铜锁支持 Bulletproofs 算法

背景

零知识证明（ZKP，Zero Knowledge Proof）是隐私计算和区块链领域中非常重要的密码学技术，能够在证明者不向验证者提供任何有用信息的情况下，使验证者相信某个论断是正确的。零知识证明于1985 年提出，至今30多年，但目前主流的零知识证明算法仅有 zk-SNARKs、zk-STARKs 和 Bulletproofs，其中 zk-SNARKs 于 2013 年提出，因其常数级的验证时间和证明大小较小，在区块链中获取了广泛的应用，但其原理非常复杂，生成证明的计算复杂度较高，还需要 trusted-setup，耦合度和复杂度都比较高，在一些场景中并不适用，zk-STARKs 解决了 zk-SNARKs 需要 trusted-setup 的问题，但其生成 zk-STARKs 的证明 size 较大，验证 zk-STARKs 的证明计算复杂度较高，不管是 zk-SNARKs 还是 zk-STARKs，门槛都比较高，而 2018年提出的 Bulletproofs 算法，其设计目标是克服传统方案的缺点并提供更高效、更紧凑的零知识证明方案。它具有以下几个优势：

• 高效性：Bulletproofs 算法具有线性的验证复杂度，这意味着验证一个证明所需的计算量与证明的大小成正比，具有较高的效率。
• 紧凑性：Bulletproofs 生成的证明相对较小，通常是输入规模的对数级别。相比于传统方案，它们更有效地传输和存储，减少了通信和存储成本。这对于在有限的计算和存储资源下进行零知识证明非常有价值。
• 通用性：Bulletproofs 是通用的，可以用于证明范围（range）和证明知识（r1cs）的零知识证明。它可以应用于各种不同的应用场景，包括Web3领域的保密交易、身份验证和隐私保护等。
• 兼容性：Bulletproofs 与现有的区块链技术兼容。它可以与现有的密码学原语和协议配合使用，如零知识范围证明（Range Proof）和加密哈希函数。这使得 Bulletproofs 能够与现有的系统和平台集成，并为其提供更高效和可靠的零知识证明能力。

综上所述，Bulletproofs 的背景是解决传统零知识证明方案的限制和缺点，它通过提供高效、紧凑和通用的证明方案来解决这些问题。Bulletproofs 具有高效性、紧凑性、通用性和兼容性等优势，使其成为在各种隐私保护和认证应用中广泛使用的零知识证明算法。目前，实现 Bulletproofs 算法的开源项目中，一是稀少，二是质量一般，三是门槛较高。铜锁作为基础密码库，非常有必要实现零知识证明算法，特别是 Bulletproofs 算法，可以将 Bulletproofs 算法应用到更多的领域，解决隐私计算和区块链中的难题。

概念

公共参数

Bulletproofs 的公共参数也有预先设置的过程，但与 zk-SNARKs 的 trusted-setup 有着较大区别，所谓 trusted-setup 是指在协议进行证明和认证之前，需要生成和设置一些公共的参数，但是在生成这些公共参数的过程中，生成了一些不能公开的中间数据，需要在完成 setup 之后把这部分不能公开的数据删除，否则任何一方拿到这些数据都能够破解协议。而 Bulletproofs 的公共参数生成叫做 setup，而不是 trusted-setup，在 Bulletproofs 的公共参数生成过程中，参与者执行特定的计算，并共享生成的公共参数，然后，其他验证者可以使用这些公共参数来验证证明的有效性。所以，证明者和验证者需要在相同的公共参数下进行，否则无法验证通过。 Bulletproofs 的公共参数主要包含两组椭圆曲线上的点，一般表示为 G 和 H，这些点生成的方式各种实现不一样，原则上只要是生成的点是椭圆曲线上的点即可，铜锁的生成方式是随机选择指定椭圆曲线上的点，而 rust 版本的 Bulletproofs 公共参数生成方式是按特定算法生成椭圆曲线上的点，这两种方式各有优劣，铜锁的生成方式更随机和通用，适应更多场景，但需要分发和共享公共参数，这些公共参数占用几 k 到几十 k 的空间，如果按特定算法生成公共参数可以不需要分发和共享，但所有场景的公共参数都一样的话可能会带来一些安全问题（这个有待考证），后面铜锁再支持按特定算法生成公共参数供用户自行选择。

证据

证据是生成证明的关键输入，证据中包含明文变量(v)和随机数(r)，以及由明文变量和随机数加密生成的密文变量（V)，Bulletproofs 论文中明确了 V 的计算公式：$V=g^vh^r$，这一步叫 Pedersen commitment，其中，证明者用到明文变量（v）和随机数（r），验证者用到密文变量（V），所以证据打包发给验证者时只需要打包密文变量 V 即可。 由于 R1CS 场景中需要将变量转换成线性约束后才能进行算术电路的运算，所以铜锁将变量实现成有名变量，方便证明者和验证者提取相关的线性约束进行算术电路的运算。需要注意的是范围证明（range proof）场景没有可变约束条件这一步，计算时会忽略证据变量中的名字，有名/无名变量都可以。

约束条件

约束条件是 R1CS 的组成部分，这些约束条件规定了输入变量之间的关系，每个约束条件都是一个等式，其中涉及到变量之间的乘法和加法运算，为了简化命令行输入和表达式解析，目前铜锁 bulletproofs 命令行只支持恒等于0的约束条件表达式，涉及到输入变量的简单约束可以在命令行完成，更复杂的逻辑运算（比如比特位判断）需要在代码中使用铜锁提供的 Bulletproofs 线性组合运算接口进行。约束条件表达式中使用的变量名必须在证据中找到提交的有名变量才行，否则报错。 约束条件是证明和验证的重要输入，对于证明者来说，需要使用证据和约束条件来计算生成相应的证明（proof），该约束条件用到的是明文证据 v 和 r，对于验证者来说，需要验证证明在该约束条件下是否有效， 该约束条件用到的是密文证据 V。

证明

证明（prove）是证明者将明文证据和约束条件计算生成一个证明对象（proof）的过程，比如证明者知道两个数 a=5 和 b=25 满足表达式 $a^2-b=0$，其中约束条件是 $a^2-b=0$，a=5 和 b=25 是有名变量，组成明文证据，a 和 b 根据密文证据公式可以计算出密文证据 a=A 和 b=B，其中 A、B 是密文，其变量名字也是 a 和 b，证明者在构造约束条件时使用的有名变量 a 和 b 用到的是明文证据 5 和 25，而验证者在构造约束条件时使用的也是有名变量 a 和 b，但用到的是密文证据 A 和 B，从而达到隐私保护的目的。 证明（prove）的输入是证据（witness）和约束条件（constraint），输出是证明对象（proof）。证明者将 proof 编码后发给验证者，验证者验证该 proof 是否有效。

验证

验证（verify）是验证者使用公共参数、密文证据、约束条件和证明对象（proof），执行 Bulletproofs 的验证算法来验证证明正确性的过程，根据验证的结果来判断证明的有效性。如果验证成功，表示陈述的真实性（即约束条件）已被证明，并且可以在不泄露陈述细节（即明文证据）的情况下确认其正确性。如果验证失败，表示陈述的真实性未能被证明，或者证明存在问题。

综上所述，可简化成如下图所示：

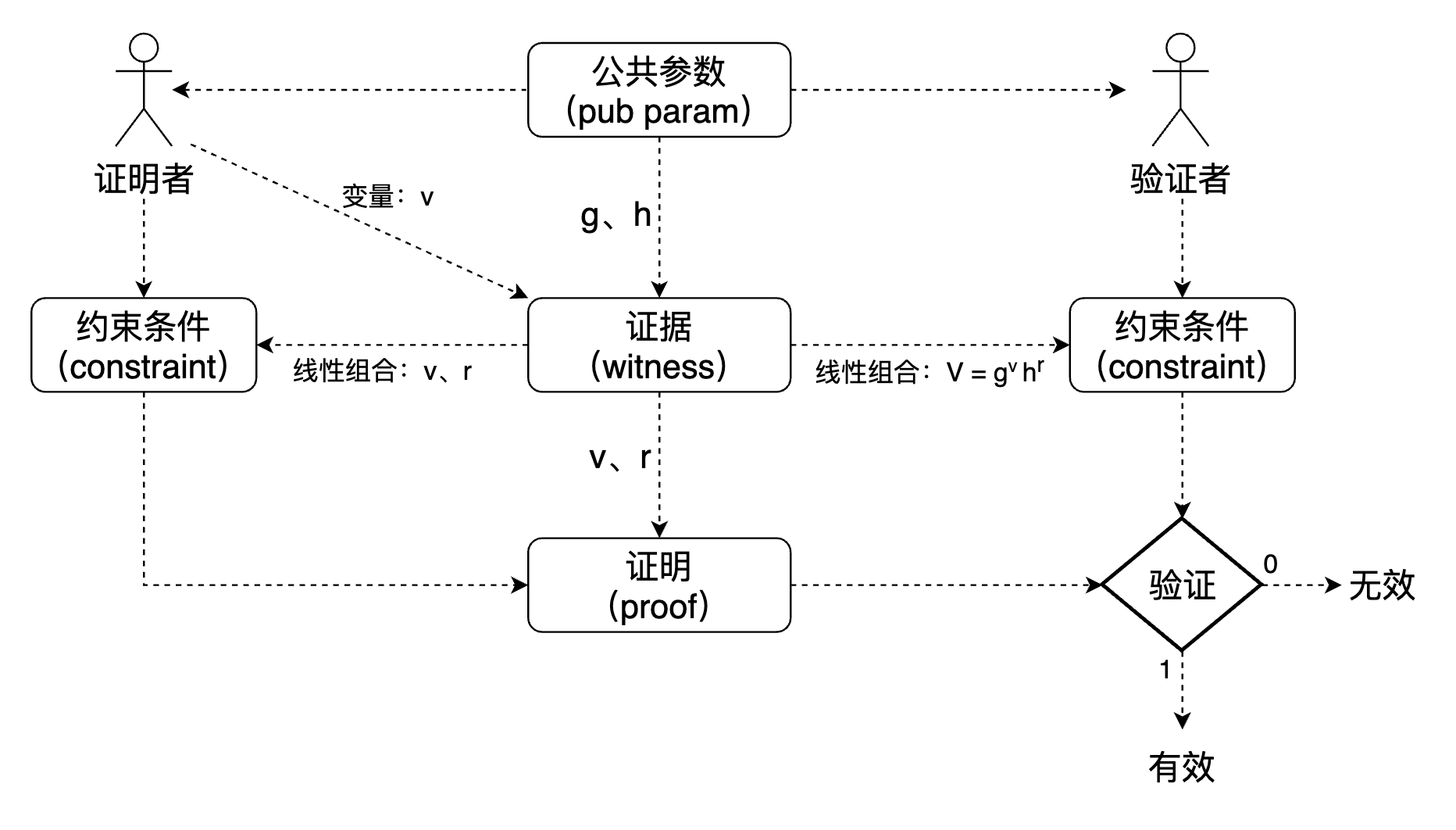
例子

铜锁为了降低零知识证明技术门槛，实现了 bulletproofs 命令行工具，通过命令行就可以体验和测试 bulletproofs，可以更好的理解和使用 bulletproofs 技术。

公共参数（-ppgen/-pp）

• 生成公共参数

$ tongsuo bulletproofs -ppgen -out ./pp.pem -curve_name sm2 -gens_capacity 16 -party_capacity 4

其中 bulletproofs 是 tongsuo 的子命令：bulletproofs 功能，不再赘述。 参数说明：

• -ppgen：是 bulletproofs 的子命令，指公共参数的生成，pp 是 pub_param 的缩写，gen 是 generate 的缩写；
• -out：输出文件路径；
• -curve_name：椭圆曲线名称；
• -gens_capacity：椭圆曲线点生成器的容量，对于 range proof 来说，该数是 range 的比特位数，对于 r1cs 来说，该数须大于约束条件表达式中乘法变量的数量；
• -party_capacity：可以生成聚合证明的最大参与方数量，仅对 range proof 有效，也就是批量范围证明的最大个数。
• 文本显示公共参数

-pp 是用来显示公共参数的子命令。

$ tongsuo bulletproofs -pp -in ./pp.pem -text -noout
Bulletproofs Public Parameter:
curve: SM2 (1172)
gens_capacity: 16
party_capacity: 4
G[n]:
    [0]: 02:b2:83:7e:13:99:e9:d7:93:57:8d:11:4a:e7:f1:01:66:0b:b2:7b:d9:2e:a4:c7:8a:bf:a6:10:89:0c:c6:93:e9
    [1]: 02:7e:44:85:96:15:53:db:f2:72:66:c5:af:b6:4d:d2:1b:f0:b7:aa:3a:f2:3a:14:fd:99:2c:e0:5d:56:26:2e:fb
    [2]: 02:81:57:f9:d5:38:f2:11:16:f4:a1:45:60:8e:50:da:31:2d:6a:c8:fa:19:d3:36:90:66:01:14:2c:14:53:0b:f0
    [3]: 03:20:46:61:ea:ff:68:49:a3:e3:d9:d5:3b:6a:a0:22:c4:78:47:c1:d0:1b:08:d7:42:8b:c9:19:d1:a8:f5:e5:18
    # 太长了，中间省略了 #
    [60]: 03:a7:b9:80:6f:ff:7d:30:6e:86:9d:d4:e0:cd:52:ee:cc:10:7e:0d:0e:6e:26:25:ae:bb:5d:48:b3:43:c0:4a:a0
    [61]: 03:4a:b8:07:7f:44:49:b2:0e:b9:26:4e:56:97:76:89:57:22:e7:34:3d:c2:e1:d9:57:a3:73:0d:dd:49:79:19:f0
    [62]: 03:9f:24:5c:30:a8:6d:08:75:8a:4c:79:04:f0:e5:41:b7:3d:41:84:71:51:77:8e:41:36:4a:9b:b6:24:bb:26:73
    [63]: 03:97:c7:a6:45:70:19:a2:ae:ff:52:fa:1c:c7:f2:e6:a0:dd:91:fd:e8:97:d8:c2:9b:4e:41:a4:9c:17:73:63:8b
H[n]:
    [0]: 03:0a:b0:b0:4c:09:7f:ec:e2:a8:41:c0:fc:75:ad:f3:02:cf:af:6a:77:a7:96:35:d8:ce:8b:6a:4b:02:a3:8c:49
    [1]: 02:5e:1d:90:be:23:90:a9:a6:02:b2:9f:b2:07:70:eb:f5:d3:0d:93:65:bd:ac:60:21:50:cc:d2:05:29:29:9d:5d
    [2]: 03:3c:d3:ef:45:77:e1:0d:e4:51:6e:73:ae:61:04:fc:6a:8d:f1:69:a6:9e:ca:d8:c4:bb:63:4c:37:c6:30:c9:05
    [3]: 03:b1:1d:fb:e0:f3:1f:33:a1:12:cf:58:0b:2c:a4:13:68:7f:42:57:98:f4:3d:0f:0c:88:98:f7:31:0e:e7:35:27
    # 太长了，中间省略了 #
    [60]: 02:bc:b6:19:81:7e:53:21:f0:b9:00:fe:b2:77:47:4c:e5:d8:f4:57:43:d0:5a:52:ba:78:59:6c:e6:00:78:23:04
    [61]: 03:cd:c2:e8:fc:27:0b:2c:af:6b:39:d7:c0:7b:2a:58:61:dd:36:8e:72:3d:6c:c1:1f:b0:12:3e:9d:78:c3:7b:cd
    [62]: 03:27:53:ec:07:b8:05:fe:24:5f:77:1d:62:c1:32:8f:75:8b:1e:bc:4f:92:ca:02:c1:ef:26:73:b3:c7:41:83:32
    [63]: 02:f0:7c:60:03:68:41:08:27:6b:d8:0b:f1:37:ba:0f:68:ac:33:f9:2b:4d:b6:74:d7:21:9f:7b:73:4c:8c:2e:90
U: 03:34:aa:13:0f:76:92:8d:33:1f:62:00:70:ff:04:86:08:9c:c7:3b:77:66:af:77:59:ce:d9:69:66:86:60:db:24
H: 02:e5:21:75:20:47:fb:c2:76:c2:86:3c:10:e0:4c:1e:72:66:26:7b:3d:5d:ac:5b:a0:de:ab:11:d3:56:bd:fc:f1

如上结果所示，G[n] 和 H[n] 就是随机生成椭圆曲线 SM2 上的点，n = gens_capacity * party_capacity，上图是64，中间一些随机点由于太长太点篇幅省略掉了。U 也是一个随机点，目前仅在 range proof 中有用，后面再看看能不能优化掉。H 一般是椭圆曲线 G 点映射到曲线上的另一个点，用来计算密文证据 $V=g^vh^r$, 公式里的 g 和 h 就是椭圆曲线的 G 点和公共参数里面的 H 点。

证据（-witness）

• 生成证据

$ tongsuo bulletproofs -witness -pp_in ./pp.pem -out witness_r1cs.pem -r1cs a=5 b=25

$ tongsuo bulletproofs -witness -pp_in ./pp.pem -out witness_range.pem 11 22 10000

$ tongsuo bulletproofs -witness -pp_in ./pp.pem -out witness_range_capacity_exceeded.pem 11 22 33 44 55

$ tongsuo bulletproofs -witness -pp_in ./pp.pem -out witness_range_exceeded.pem 65536

参数说明：

• -witness：是用来生成/显示证据的子命令
• -pp_in：指定公共参数文件所在路径
• -out：生成的证据文件路径，上述四条命令生成的四个证据文件分别为：
  • witness_r1cs.pem：r1cs 证据文件
  • witness_range.pem：正常的 range 证据文件
  • witness_range_capacity_exceeded.pem：容量超出的证据文件，因为生成的公共参数支持的批量证明和验证个数为最多4个，这里指定了5个，在生成证明时会报错
  • witness_range_exceeded.pem：range 范围超出的证据文件，因为生成的公共参数可证明和验证的二进制比特位为16，验证范围是 $[0, 2^{16})$，也就是 0-65535，提交的 65536 在验证时会失败。
• -r1cs：是指定生成的是 r1cs 证据，否则生成的是 range proof 的证据
• a=5 b=25 是有名变量，多个变量用空格隔开，=号前面是变量名，=号后面是变量值，目前仅支持整数（正/负均可），如果是 range proof 的证据，可以不需要指定变量名，直接输入变量值用空格分开即可，需要注意的是如果是负数需要用有名变量的方式来指定，否则解析报错，有负数的情况可以这么输入：11 22 xx=-33 44
• 显示证据

$ tongsuo bulletproofs -witness -in witness_r1cs.pem -text
Witness:
curve: SM2 (1172)
H: 02:e5:21:75:20:47:fb:c2:76:c2:86:3c:10:e0:4c:1e:72:66:26:7b:3d:5d:ac:5b:a0:de:ab:11:d3:56:bd:fc:f1
V[n]:
    [a]: 02:2d:2e:29:b9:cf:1e:86:03:a4:7a:67:91:b8:25:62:84:65:b0:03:19:8e:fb:d1:ee:1d:af:dc:bc:da:01:3b:cb
    [b]: 03:c9:18:b7:b1:47:c5:db:0c:b9:55:64:a4:c0:0d:fe:d2:a0:03:3d:11:53:66:2f:7a:dd:c9:a6:e4:6a:01:5f:ca
v[n]:
    [a]: 5 (0x5)
    [b]: 25 (0x19)
r[n]:
    [0]: 00:a2:b2:0d:e5:78:2a:dc:c1:97:1f:52:8a:6f:4b:ad:fc:22:ce:d2:33:7a:71:c3:f1:be:15:d2:f8:2d:c1:f9:19
    [1]: 00:ba:4d:82:79:57:7f:d7:8a:42:a8:40:a8:52:d4:2a:32:91:a1:37:fe:dc:61:a3:a9:f4:05:c1:5e:54:4b:d6:bb
-----BEGIN BULLETPROOFS WITNESS-----
AAAElALlIXUgR/vCdsKGPBDgTB5yZiZ7PV2sW6DeqxHTVr388QAAAAICLS4puc8e
hgOkemeRuCVihGWwAxmO+9HuHa/cvNoBO8thAAPJGLexR8XbDLlVZKTADf7SoAM9
EVNmL3rdyabkagFfymIAAAAAAiuisg3leCrcwZcfUopvS638Is7SM3pxw/G+FdL4
LcH5GSu6TYJ5V3/XikKoQKhS1CoykaE3/txho6n0BcFeVEvWuwAAAAIrAAAAAAAA
AAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAUrAAAAAAAAAAAAAAAAAAAAAAAAAAAA
AAAAAAAAAAAAABk=
-----END BULLETPROOFS WITNESS-----

$ tongsuo bulletproofs -witness -in witness_range.pem -text
Witness:
curve: SM2 (1172)
H: 02:e5:21:75:20:47:fb:c2:76:c2:86:3c:10:e0:4c:1e:72:66:26:7b:3d:5d:ac:5b:a0:de:ab:11:d3:56:bd:fc:f1
V[n]:
    [0]: 03:a0:80:74:69:3a:9e:ad:d3:c2:f2:8f:90:db:34:11:89:b5:ab:2a:da:e5:e5:45:1c:0a:e3:63:86:f2:0e:92:13
    [1]: 02:1b:1d:6a:c4:e5:ae:80:19:0c:0d:ce:48:bf:7e:19:c1:b3:a2:9a:ce:da:d1:40:dc:bd:de:43:b4:e3:c8:6a:14
    [2]: 02:b3:76:ca:f5:0a:fc:37:9d:dd:55:52:37:f7:2c:4e:a4:9c:91:41:f4:d0:ea:2e:64:05:2e:dd:f7:fb:0a:1b:1d
v[n]:
    [0]: 11 (0xb)
    [1]: 22 (0x16)
    [2]: 10000 (0x2710)
r[n]:
    [0]: 4d:df:5b:b7:fb:ed:73:1a:cc:40:53:19:4f:35:e8:f5:bf:f8:08:30:cc:6d:f7:25:77:87:f1:a4:87:1e:d8:ea
    [1]: 57:cb:b6:2a:db:b5:5c:e9:33:27:73:88:72:b4:18:18:1e:da:41:b1:71:32:8f:29:f4:e7:cc:c7:a4:f3:3b:31
    [2]: 00:88:b0:2c:3f:a0:4d:8a:91:1e:fa:3c:9b:0a:c2:e0:b1:89:7a:b4:b2:2c:e6:50:75:f7:61:60:d3:2c:b9:33:94
-----BEGIN BULLETPROOFS WITNESS-----
AAAElALlIXUgR/vCdsKGPBDgTB5yZiZ7PV2sW6DeqxHTVr388QAAAAMDoIB0aTqe
rdPC8o+Q2zQRibWrKtrl5UUcCuNjhvIOkhMAAhsdasTlroAZDA3OSL9+GcGzoprO
2tFA3L3eQ7TjyGoUAAKzdsr1Cvw3nd1VUjf3LE6knJFB9NDqLmQFLt33+wobHQAA
AAADK03fW7f77XMazEBTGU816PW/+AgwzG33JXeH8aSHHtjqK1fLtirbtVzpMydz
iHK0GBge2kGxcTKPKfTnzMek8zsxK4iwLD+gTYqRHvo8mwrC4LGJerSyLOZQdfdh
YNMsuTOUAAAAAysAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAACysAAAAA
AAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAFisAAAAAAAAAAAAAAAAAAAAAAAAA
AAAAAAAAAAAAAAAnEA==
-----END BULLETPROOFS WITNESS-----

如上结果所示，witness 中包含了椭圆曲线名称，H 点（与公共参数一致），密文证据 V，明文证据 v 和随机数 r。有名变量会在括号中显示变量名，无名变量直接显示索引号。

证明（-prove/-proof）

• 生成 r1cs 证明（-prove）

$ tongsuo bulletproofs -prove -pp_in ./pp.pem -witness_in witness_r1cs.pem -out proof-r1cs.pem -r1cs_constraint "a*a-b"

$ tongsuo bulletproofs -prove -pp_in ./pp.pem -witness_in witness_r1cs.pem -out proof-r1cs.pem -r1cs_constraint "a*a-c"
May be extra arguments error, please use -help for usage summary.
80C5990001000000:error:1F800070:lib(63):bp_r1cs_expression_evaluate_variable:reason(112):crypto/zkp/bulletproofs/r1cs_constraint_expression.c:266:
80C5990001000000:error:1F80006F:lib(63):bp_r1cs_expression_process:reason(111):crypto/zkp/bulletproofs/r1cs_constraint_expression.c:302:

参数说明：

• -pp_in：指定公共参数文件所在路径
• -witness_in：指定证据文件所在路径
• -out：指定证明的输出路径，输出的文件包含两段：R1CS PROOF 和 WITNESS，分别为 proof 和 witness
• -r1cs_constraint：指定约束条件，里面引用的变量必须在生成证据时提交的变量名中，否则报错，如上述第二条命令所示
• 生成 range 证明（-prove）：不用加 -r1cs_constraint 即可

$ tongsuo ./apps/openssl bulletproofs -prove -pp_in ./pp.pem -witness_in witness_range.pem -out proof-range.pem

$ tongsuo bulletproofs -prove -pp_in ./pp.pem -witness_in witness_range_exceeded.pem -out proof-range-exceeded.pem

$ tongsuo ./apps/openssl bulletproofs -prove -pp_in ./pp.pem -witness_in witness_range_capacity_exceeded.pem -out proof-range-capacity-exceeded.pem
May be extra arguments error, please use -help for usage summary.
80C54E0201000000:error:1F800068:lib(63):BP_RANGE_PROOF_prove:reason(104):crypto/zkp/bulletproofs/range_proof.c:276:

由证据文件 witness_range.pem、proof-range-exceeded.pem 和 proof-range-capacity-exceeded.pem 分别生成相应的 range proof，可以看出，超出批量容量个数的证据生成证明时报错了。

• 显示证明（-proof）

$ tongsuo bulletproofs -proof -in proof-r1cs.pem -text
R1CS Proof:
AI1: 03:7f:62:d5:d4:7a:7a:91:3b:98:9f:73:c7:d6:9b:29:7e:5d:df:a0:09:f7:f7:a1:0f:f4:e6:dd:47:4a:5c:8f:bf
AO1: 03:6a:98:d0:66:09:9c:f1:ee:5d:ac:e8:df:ac:6d:08:c2:46:6a:4c:7f:5c:ec:86:df:45:a1:99:6f:1f:7c:57:c4
S1: 03:57:b0:23:16:dc:81:61:df:89:dc:b2:ff:0b:61:8d:4e:f1:fd:e2:08:c2:f8:11:25:d4:86:ea:41:04:aa:66:c9
AI2: 00:00:00:00:00:00:00:00:00:00:00:00:00:00:00:00:00:00:00:00:00:00:00:00:00:00:00:00:00:00:00:00:00
AO2: 00:00:00:00:00:00:00:00:00:00:00:00:00:00:00:00:00:00:00:00:00:00:00:00:00:00:00:00:00:00:00:00:00
S2: 00:00:00:00:00:00:00:00:00:00:00:00:00:00:00:00:00:00:00:00:00:00:00:00:00:00:00:00:00:00:00:00:00
T1: 03:68:73:93:9b:69:90:c9:26:4e:dc:fb:a4:cb:40:8a:fd:38:e0:40:00:aa:87:d2:a3:13:0a:c3:1a:45:b2:49:14
T3: 03:8a:39:19:dc:40:80:53:f2:3b:99:fa:3c:de:e1:3d:ad:0d:f7:b3:f6:ab:f9:bb:38:58:fa:19:76:c1:d2:96:7c
T4: 03:04:3e:f7:1a:bc:98:97:36:28:25:02:a5:38:30:da:b7:ff:c9:83:16:dc:2f:86:8a:33:d5:a0:c3:a3:78:7b:c7
T5: 03:54:2e:62:c9:ca:6c:d0:51:66:19:b5:a7:1e:0c:da:7b:22:1c:14:32:b4:5a:b2:12:c6:fc:05:ba:f0:62:77:5e
T6: 03:95:db:79:ee:f3:db:b8:b0:46:fb:39:f8:59:d7:23:2a:d7:f1:42:c3:95:15:79:6a:82:8e:a2:37:87:17:c3:b1
taux: 29:b6:03:b5:46:eb:2c:c3:c1:90:14:d4:20:41:8c:34:d1:83:7e:fc:02:83:7c:76:00:ed:f1:9d:2c:11:16:d4
mu: 00:ff:ba:a7:01:7f:d0:96:25:7a:06:e4:7f:ae:45:b6:3a:e4:aa:1c:38:34:b9:d6:1a:a6:60:93:38:aa:0c:89:69
tx: 00:b8:c8:56:04:ac:0e:9e:c3:f6:d9:fd:c9:4c:2a:5a:29:da:0a:87:c4:2e:c8:5a:97:ca:b6:45:a6:30:2c:ac:d1
inner proof:
    n: 0
    L[n]:
    R[n]:
    a: 00:ca:ab:e9:fa:45:79:de:d5:17:c0:dc:12:c5:da:d2:22:04:53:a1:45:de:e4:dd:97:bc:c0:ca:67:a8:6b:53:fc
    b: 00:ca:3b:1b:91:b9:47:a1:fd:24:05:ac:e9:05:82:19:d7:8d:b1:08:03:79:42:25:ec:ed:c5:e7:0c:ba:b2:a4:8a
-----BEGIN BULLETPROOFS R1CS PROOF-----
AAAElAAAAAgDf2LV1Hp6kTuYn3PH1pspfl3foAn396EP9ObdR0pcj78DapjQZgmc
8e5drOjfrG0IwkZqTH9c7IbfRaGZbx98V8QDV7AjFtyBYd+J3LL/C2GNTvH94gjC
+BEl1IbqQQSqZskDaHOTm2mQySZO3Puky0CK/TjgQACqh9KjEwrDGkWySRQDijkZ
3ECAU/I7mfo83uE9rQ33s/ar+bs4WPoZdsHSlnwDBD73GryYlzYoJQKlODDat//J
gxbcL4aKM9Wgw6N4e8cDVC5iycps0FFmGbWnHgzaeyIcFDK0WrISxvwFuvBid14D
ldt57vPbuLBG+zn4WdcjKtfxQsOVFXlqgo6iN4cXw7EAAAADKym2A7VG6yzDwZAU
1CBBjDTRg378AoN8dgDt8Z0sERbUK/+6pwF/0JYlegbkf65Ftjrkqhw4NLnWGqZg
kziqDIlpK7jIVgSsDp7D9tn9yUwqWinaCofELshal8q2RaYwLKzRAAAAAivKq+n6
RXne1RfA3BLF2tIiBFOhRd7k3Ze8wMpnqGtT/CvKOxuRuUeh/SQFrOkFghnXjbEI
A3lCJeztxecMurKkigAAAAAAAAAA
-----END BULLETPROOFS R1CS PROOF-----
Witness:
curve: SM2 (1172)
H: 02:e5:21:75:20:47:fb:c2:76:c2:86:3c:10:e0:4c:1e:72:66:26:7b:3d:5d:ac:5b:a0:de:ab:11:d3:56:bd:fc:f1
V[n]:
    [a]: 02:2d:2e:29:b9:cf:1e:86:03:a4:7a:67:91:b8:25:62:84:65:b0:03:19:8e:fb:d1:ee:1d:af:dc:bc:da:01:3b:cb
    [b]: 03:c9:18:b7:b1:47:c5:db:0c:b9:55:64:a4:c0:0d:fe:d2:a0:03:3d:11:53:66:2f:7a:dd:c9:a6:e4:6a:01:5f:ca
-----BEGIN BULLETPROOFS WITNESS-----
AAAElALlIXUgR/vCdsKGPBDgTB5yZiZ7PV2sW6DeqxHTVr388QAAAAICLS4puc8e
hgOkemeRuCVihGWwAxmO+9HuHa/cvNoBO8thAAPJGLexR8XbDLlVZKTADf7SoAM9
EVNmL3rdyabkagFfymIA
-----END BULLETPROOFS WITNESS-----

$ tongsuo bulletproofs -proof -in proof-range.pem -text
Range Proof:
A: 03:03:29:b3:64:40:02:99:1a:4d:22:4d:af:4e:6c:8d:14:84:e7:6a:94:05:bd:91:57:d0:40:7a:c1:fe:e5:96:94
S: 03:12:46:e0:97:01:a2:d6:bf:ea:90:5c:01:2c:0c:fe:ae:5f:8a:da:38:ce:0e:6c:29:a4:08:46:fb:34:ed:5b:ed
T1: 02:c3:0b:2d:49:8f:b1:e5:bb:2a:d6:40:51:8a:2c:6a:58:d8:59:0c:87:f1:e4:b4:81:f5:b1:a3:2d:d6:90:7e:60
T2: 02:eb:34:90:10:ed:b1:32:99:9f:1f:ff:09:7a:d3:15:4c:be:34:69:59:48:a4:fd:4b:e5:70:2a:d1:7a:30:9b:82
taux: 38:e7:c2:84:3c:16:c3:8e:7d:5e:8d:38:d5:8b:8e:4a:8e:45:95:db:e3:49:87:7f:36:63:b8:fb:6a:e8:0b:c4
mu: 00:b8:29:e5:f8:75:a3:32:f6:38:23:40:2e:90:ec:35:b0:84:2a:00:1d:04:6b:2e:67:53:50:ec:c0:98:ff:79:6b
tx: 00:8f:46:12:73:9d:e6:cb:aa:3e:21:4b:4d:f8:b4:66:91:40:fd:7e:bb:c0:b5:f7:07:ce:a5:f2:ff:98:86:62:40
inner proof:
    n: 6
    L[n]:
        [0]: 02:e7:34:ca:e7:98:a6:52:a6:83:ce:62:a6:c0:50:ec:86:4b:98:e9:19:c7:54:07:3d:d5:e3:f5:8d:fb:50:e0:c5
        [1]: 03:53:38:d4:99:6d:7d:cd:88:88:e5:92:b2:ce:13:f4:ce:3b:fe:e2:5f:12:c5:4b:d0:93:83:b6:35:fd:0d:03:24
        [2]: 03:a6:f9:93:14:b2:46:02:34:96:08:39:d2:28:65:83:1e:27:20:96:b1:e5:e7:f8:1f:a6:7a:9e:e7:df:60:e2:79
        [3]: 02:f4:b5:c4:76:a5:5e:c0:69:c5:a2:4d:24:52:9a:90:87:e3:cc:2a:3d:52:0b:3e:58:24:2e:c7:66:4e:65:b3:cf
        [4]: 03:44:5b:eb:8f:1c:91:a1:7f:9e:a7:9b:ed:fb:52:81:90:3a:4a:dc:1d:ee:dd:6b:66:71:c2:14:3c:7a:d4:c3:03
        [5]: 03:b7:53:59:4d:69:cf:12:85:41:52:60:f9:d2:c2:a1:82:88:6e:af:f3:33:f6:36:55:eb:99:61:ac:37:7d:c4:74
    R[n]:
        [0]: 03:08:3d:7c:3c:21:7f:7f:79:bb:43:05:ec:0b:76:41:9f:54:13:d0:c9:2d:7a:23:67:91:92:7f:74:ce:3e:ef:04
        [1]: 02:a7:f1:f2:de:ad:89:7c:1a:17:06:df:59:81:9f:9e:93:51:22:19:a7:74:9a:30:6c:ca:e8:6b:c5:8b:c2:6f:85
        [2]: 02:fc:0a:45:3b:86:37:a0:fd:6a:8f:92:0a:30:b9:2d:99:c5:2c:89:20:40:23:39:58:b0:da:f4:de:0c:5c:2a:ad
        [3]: 02:da:69:0e:87:f5:57:8d:a1:44:c7:9a:40:d2:d3:f5:aa:c1:e1:08:5c:fd:d4:37:9a:75:8a:9b:4e:2f:fe:56:79
        [4]: 02:35:7c:29:a0:47:17:84:71:ed:9c:bd:ed:9e:fc:9f:83:81:33:9d:c0:30:15:54:6f:53:f0:49:79:6d:a4:60:51
        [5]: 03:a0:88:ec:8a:de:4a:59:78:a7:f4:c9:5d:9a:a0:b9:ab:58:93:61:22:ef:ec:66:5c:1e:53:f1:a3:d6:bb:eb:b3
    a: 00:bb:f6:3c:a4:5c:d8:8e:7c:a6:fc:e1:c6:68:83:b3:67:49:b0:1e:a4:0d:1c:43:8d:a9:21:49:f2:cc:97:70:6e
    b: 00:98:f8:f1:9e:fd:5c:3d:39:2f:cf:4b:f4:78:2d:3d:26:1b:ca:cc:35:25:17:d6:ca:78:65:34:f4:65:81:fa:5b
-----BEGIN BULLETPROOFS RANGE PROOF-----
AAAElAAAAAQDAymzZEACmRpNIk2vTmyNFITnapQFvZFX0EB6wf7llpQDEkbglwGi
1r/qkFwBLAz+rl+K2jjODmwppAhG+zTtW+0CwwstSY+x5bsq1kBRiixqWNhZDIfx
5LSB9bGjLdaQfmAC6zSQEO2xMpmfH/8JetMVTL40aVlIpP1L5XAq0Xowm4IAAAAD
KzjnwoQ8FsOOfV6NONWLjkqORZXb40mHfzZjuPtq6AvEK7gp5fh1ozL2OCNALpDs
NbCEKgAdBGsuZ1NQ7MCY/3lrK49GEnOd5suqPiFLTfi0ZpFA/X67wLX3B86l8v+Y
hmJAAAAAAiu79jykXNiOfKb84cZog7NnSbAepA0cQ42pIUnyzJdwbiuY+PGe/Vw9
OS/PS/R4LT0mG8rMNSUX1sp4ZTT0ZYH6WwAAAAYC5zTK55imUqaDzmKmwFDshkuY
6RnHVAc91eP1jftQ4MUDUzjUmW19zYiI5ZKyzhP0zjv+4l8SxUvQk4O2Nf0NAyQD
pvmTFLJGAjSWCDnSKGWDHicglrHl5/gfpnqe599g4nkC9LXEdqVewGnFok0kUpqQ
h+PMKj1SCz5YJC7HZk5ls88DRFvrjxyRoX+ep5vt+1KBkDpK3B3u3WtmccIUPHrU
wwMDt1NZTWnPEoVBUmD50sKhgohur/Mz9jZV65lhrDd9xHQAAAAGAwg9fDwhf395
u0MF7At2QZ9UE9DJLXojZ5GSf3TOPu8EAqfx8t6tiXwaFwbfWYGfnpNRIhmndJow
bMroa8WLwm+FAvwKRTuGN6D9ao+SCjC5LZnFLIkgQCM5WLDa9N4MXCqtAtppDof1
V42hRMeaQNLT9arB4Qhc/dQ3mnWKm04v/lZ5AjV8KaBHF4Rx7Zy97Z78n4OBM53A
MBVUb1PwSXltpGBRA6CI7IreSll4p/TJXZqguatYk2Ei7+xmXB5T8aPWu+uz
-----END BULLETPROOFS RANGE PROOF-----
Witness:
curve: SM2 (1172)
H: 02:e5:21:75:20:47:fb:c2:76:c2:86:3c:10:e0:4c:1e:72:66:26:7b:3d:5d:ac:5b:a0:de:ab:11:d3:56:bd:fc:f1
V[n]:
    [0]: 03:a0:80:74:69:3a:9e:ad:d3:c2:f2:8f:90:db:34:11:89:b5:ab:2a:da:e5:e5:45:1c:0a:e3:63:86:f2:0e:92:13
    [1]: 02:1b:1d:6a:c4:e5:ae:80:19:0c:0d:ce:48:bf:7e:19:c1:b3:a2:9a:ce:da:d1:40:dc:bd:de:43:b4:e3:c8:6a:14
    [2]: 02:b3:76:ca:f5:0a:fc:37:9d:dd:55:52:37:f7:2c:4e:a4:9c:91:41:f4:d0:ea:2e:64:05:2e:dd:f7:fb:0a:1b:1d
    [3]: 02:0d:30:77:fb:4f:a5:f6:7d:e4:78:f3:84:ca:96:28:c2:46:92:df:2b:dc:57:f7:f8:8b:8a:33:63:c9:6d:91:7b
-----BEGIN BULLETPROOFS WITNESS-----
AAAElALlIXUgR/vCdsKGPBDgTB5yZiZ7PV2sW6DeqxHTVr388QAAAAQDoIB0aTqe
rdPC8o+Q2zQRibWrKtrl5UUcCuNjhvIOkhMAAhsdasTlroAZDA3OSL9+GcGzoprO
2tFA3L3eQ7TjyGoUAAKzdsr1Cvw3nd1VUjf3LE6knJFB9NDqLmQFLt33+wobHQAC
DTB3+0+l9n3kePOEypYowkaS3yvcV/f4i4ozY8ltkXsA
-----END BULLETPROOFS WITNESS-----

可以看出 proof-r1cs.pem 中包含了两段：R1CS PROOF 和 WITNESS，这里 WITNESS 的 V 就是密文证据。

验证（-verify）

$ tongsuo bulletproofs -verify -pp_in ./pp.pem -in proof-r1cs.pem -r1cs_constraint "a*a-b"
The proof is valid

$ tongsuo bulletproofs -verify -pp_in ./pp.pem -in proof-r1cs.pem -r1cs_constraint "a*a-b+a*a-b"
The proof is invalid

$ tongsuo bulletproofs -verify -pp_in ./pp.pem -in proof-r1cs.pem -r1cs_constraint "a*5-b"
The proof is invalid

$ tongsuo bulletproofs -verify -pp_in ./pp.pem -in proof-range.pem
The proof is valid

$ tongsuo bulletproofs -verify -pp_in ./pp.pem -in proof-range-exceeded.pem
The proof is invalid

验证 r1cs 的 proof 时需要指定相同的约束条件参数（-r1cs_constraint），否则验证失败。需要注意的是表达式一定要一致，即使 a 和 b 的其他运算也能为0，但不一致的约束条件会导致内部运算逻辑与 prove 不一致而验证失败。 如上结果，可以看出，与 prove 一致的约束条件的验证结果有效，其他无效，在范围内的 proof 验证结果有效，超出范围的验证无效。

接口说明

接口文档正在编写中，敬请期待后续系列文章。